Mates 1 Eco. Solución 2º Parcial Dic 2018
Aquí tienes las soluciones de los distintos ejercicios del grupo Eco-1:
1. (2 puntos) Dada la función \(f(x)=x^2+3x+1\), contesta razonadamente a las siguientes preguntas:
1.1 Calcula la pendiente de la recta tangente a la gráfica de la función en el punto \(x=-1\).
Solution
\(m=f'(-1)=1\)
1.2. Calcula la ecuación de la recta tangente a la gráfica de la función en el punto \(x = -1\).
Solución
\(y=x\)
1.3. Calcula la ecuación de la recta paralela a la del apartado anterior que pasa por el punto (1,-2).
Solución
\(y=x+3\)
1.4. Calcula la ecuación de la recta perpendicular a la adel apartado anterior que pasa por el punto (-1,2).
Solución
\(y=-x+1\)
1.5. Dibuja las rectas de los apartados anteriores
1.6. ¿Para qué valor de \(x\) la recta tangente a la gráfica de \(f(x)\) en ese punto es paralela a la recta \(2y-6x+15=0\)?
Solución
\(x=0\)
2. (2 puntos) Dada la función \(f (x) =\sqrt{ (x^2 — 1)(x + 3)}\), contesta razonadamente las siguientes preguntas:
2.1. Calcula el dominio de \(f (x)\).
Solución
\([-3,-1]\cup [1,+\infty]\)
2.2. En caso de que existan, da las ecuaciones de las asíntotas horizontales y verticales de \(f (x)\).
Solución
No tiene asíntotas horizontales no verticales
2.3. Enuncia el teorema de Bolzano. ¿Se puede aplicar a la función \(f (x)\) en el intervalo [0, 6]?
Solución
No se puede aplicar porque la función no es continua en [0,6], pues el subintervalo [0,1) no pertenece al dominio de la función.
2.4. Calcula \(f'(2)\).
Solución
\(f'(2)=\dfrac{23}{2\sqrt{15}}\)
2.5. Dada la función \(g(x) = x^2 + 1\), calcula \(g \circ f\) y\( f \circ g\).
Solución
\(g \circ f=x^3+3x^2-x-2\)
\(f \circ g=\sqrt{x^6+6x^4+8x^2}\)
2.6. Calcula \(g^{-1}(x)\) e indica cuál es su dominio.
Solución
\(g^{-1}(x)=\pm \sqrt{x-1}\)
Dominio: \(x-1\geq 0 \rightarrow x\geq 1\)
3. (2 puntos) Dada la función \(f (x) = x ln(x) — x\), definida en su dominio \(D = (0, +1)\), contesta razonadamente a las siguientes preguntas:
3.1. Calcula \(\displaystyle{\int f (x) dx}\).
Solución
\(\dfrac{x^2}{2}\ln x-\dfrac{3}{4}x^2+C\)
3.2. Calcula \(\displaystyle{\lim_{x \to 0} f(x)}\).
Solución
\(\displaystyle{\lim_{x \to 0} f(x)=0}\)
3.3. Calcula las zonas de crecimiento y decrecimiento de \(f (x)\).
Solución
Decreciente en \([0,1)\)
Creciente en \((1,+\infty)\)
3.4. ¿Tiene la función máximos y/o mínimos locales? En caso afirmativo, ¿en qué puntos se alcanzan?
Solución
Mínimo relativo en \(x=1\) luefo el punto es el \((1,-1)\)
3.5. Calcula las zonas de concavidad y convexidad de \(f (x)\).
Solución
La función es siempre convexa
3.6. ¿Cuál de las siguientes gráficas corresponde con la de la función \(f (x)\)? ¿Por qué?.
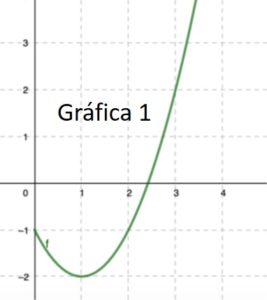
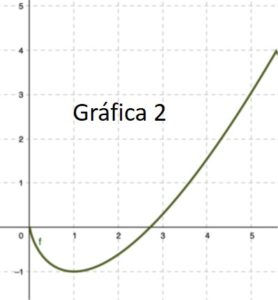
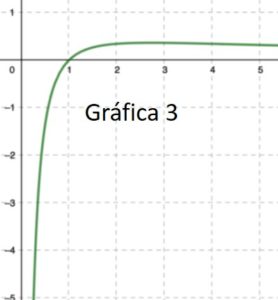
Solución
La gráfica 1. Es la que cumple todos las condiciones que hemos visto
4. (2 puntos) La siguiente figura proporciona la gráfica de \(f'(x)\), que es la derivada de una función
desconocida \(f(x)\). Contesta razonadamente las siguientes preguntas:
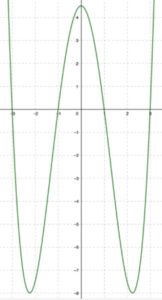
4.1. Razona las zonas de crecimiento y decrecimiento de \(f(x)\).
Solución
Creciente en \( (-\infty,-3)\)
Decreciente en \((-3,-1)\)
Creciente en \((-1,1)\)
Decreciente en \((1,3)\)
Creciente en \((3,+\infty)\)
4.2. Razona dónde alcanza \(f(x)\) máximos y/o mínimos locales.
Solución
Máximo local en \(x=-3\)
Mínimo local en \(x=-1\)
Máximo local en \(x=1\)
Mínimo local en \(x=3\)
4.3. Razona la concavidad o convexidad de \(f(x)\) en el intervalo \((-\infty,-3)\).
Solución
\(f(x)\) convexa en el intervalo \((-\infty,-3)\).
4.4. Si se sabe la ecuación de la derivada es \(f'(x) = \dfrac{1}{2}x^4 – 5x^2 + \dfrac{9}{2}\) y que \(f(0) = 0\), calcula \(f(x)\).
Solución
\(y=\dfrac{1}{10}x^5-\dfrac{5}{3}x^3+\dfrac{9}{2}x\)
4.5. Calcula el valor de la integral \(\displaystyle{\int_{0}^{1} f'(x) dx}\)
Solución
\(\displaystyle{\int_{0}^{1} f'(x) dx=\dfrac{1}{10}-\dfrac{5}{3}+\dfrac{9}{2}=\dfrac{44}{15}\approx 2.933}\)
4.6. Calcula el área entre \(f'(x)\) y el eje \(X\) en el intervalo [0, 2].
Solución
7 unidades
5. (2 puntos) Contesta razonadamente las siguientes preguntas:
5.1. Calcula la primitiva de la función \(f(x) = 2xe^{x^2}\).
Solución
\(F(x)=\displaystyle{\int} f(x) dx=\displaystyle{e^{x^2}}+C\)
5.2. Calcula la primitiva de la función \(f(x) = xe^x\).
Solución
\(F(x)=\displaystyle{\int} f(x) dx=e^x(x-1)+C\)
5.3. Calcula, si es convergente, el valor de la integral impropia \(\displaystyle{\int_{-\infty}^{1}xe^x dx}\).
Solución
\(\displaystyle{\int_{-\infty}^{1}xe^x dx=0}\)
5.4. Calcula el área encerrada entre las funciones \(f(x) = x^2\) y \(g(x) = e^x\) en el intervalo [0, 1].
Solución
Área encerrada=\(e-\dfrac{4}{3}\)
5.5. Calcula el intervalo abierto de convergencia de la serie de potencias \(\displaystyle{\sum_{i=1}^{\infty}\dfrac{n}{2^n}x^n}\).
Solución
\((-2,2)\)
5.6. Indica la razón de la serie geométrica \(\displaystyle{\sum_{i=2}^{\infty}\dfrac{(-1)^n}{3^{2n}}}\)y, en caso de que sea convergente, calcula su suma.
Solución
\(r=\left(-\dfrac{1}{9}\right)\)
\(\displaystyle{\sum_{i=2}^{\infty}\dfrac{(-1)^n}{3^{2n}}=\dfrac{1}{90}}\)
