Mates 1 Eco. Solución 2º Parcial Dic 2018. Grupo 3
Aquí tienes las soluciones del 2º parcial de mates 1 de diciembre de 2018.
1. (2 puntos) Dada la función \(f(x) =\dfrac{2x}{x^2-3}\)
1.1. Calcula la ecuación de la recta tangente a la gráfica de \(f(x)\) en el punto \(x = 0\).
Solución
\(y=-\dfrac{2}{3}x\)
1.2. Calcula la ecuación de la recta paralela a la anterior que pase por (1,-1).
Solución
\(y=-\dfrac{2}{3}x-\dfrac{1}{3}\)
1.3. Calcula la ecuación de la recta perpendicular a la del apartado 1.1 que pasa por (1,-1).
Solución
\(y=\dfrac{3}{2}x-\dfrac{5}{2}\)
1.4. Calcula las zonas de crecimiento y decrecimiento de \(f(x)\).
Solución
\(f(x)\) es siempre decreciente en su dominio
1.5. Calcula una primitiva de \(f(x)\).
Solución
\(F(x)=\ln (x^2-3)+C\)
1.6. Calcula \(\displaystyle{\int_{2}^{5}f(x) dx}\)
Solución
\(\displaystyle{\int_{2}^{5}f(x) dx=\ln 22}\)
2. (2 puntos) Dada la función \(f(x)=\left\{\begin{matrix}
2e^{ax^2-a} &si &x \leq 1 \\
bx^2& si & x>1
\end{matrix}\right.\)
2.1. Si \(b = -2\), calcula un punto x mayor que 1 en el que la recta tangente a la gráfica de la función sea paralela a la recta \(16x + 2y = 5\). ¿Cuál es la ecuación de dicha recta tangente?
Solución
\(x=2\)
\(y(2)=-8x+8\)
2.2. Si \(a = -1\), ¿la función \(f(x)\) es creciente o decreciente en el intervalo (-1, 0)? Razona la respuesta.
Solución
Creciente al ser \(f'(-1)>0\)
2.3. Si \(b = -1\), ¿la función \(f(x)\) es cóncava o convexa en el intervalo (1,+1)? Razona la respuesta.
Solución
Cóncava siempre al ser \(f»(x)=-2 \)
2.4. Calcula los valores de \(a\) y \(b\) para que la función \(f(x)\) sea continua y derivable en x = 1.
Solución
\(a=1. \ b=2\)
2.5. Enuncia el teorema de Rolle. Con los valores de \(a\) y \(b\) calculados en el apartado 2.4, ¿se puede aplicar este teorema en el intervalo [0, 2]? Razona la respuesta.
Solución
Se puede aplicar en cualquier inbtervalo pues los valores de \(a\) y \(b\) hallados aseguran la continuidad y la derivabilidad
2.6. Enuncia el teorema de Bolzano. Con los valores de \(a\) y \(b\) calculados en el apartado 2.4, ¿se podría aplicar en algún intervalo?. Razona la respuesta.
Solución
No se puede aplicar, pues la función no cambia de signo, al ser siempre positiva.
3. (2 puntos) Dada la función \(f(x) = ln((x – 1)(x + 3))\), contesta razonadamente las siguientes preguntas:
3.1. Calcula el dominio de \(f(x)\).
Solución
\(Dom\{f(x)\}=(-\infty,-3) \cup (1,+\infty )\)
3.2. En caso de que existan, da las ecuaciones de las asíntotas verticales de \(f(x)\).
Solución
\(x=-3^-\) AV hacia \(-\infty\)
\(x=+1^+\) AV hacia \(-\infty\)
3.3. Calcula \(f'(2)\).
Solución
\(f'(2)=\dfrac{6}{5}\)
3.4. Calcula las zonas de crecimiento y decrecimiento de \(f(x)\).
Solución
Decreciente en \((-\infty,-3)\)
Creciente en \( (1,+\infty)\)
3.5. Calcula \(g \circ f\), siendo \(g(x) = e^x\).
Solución
\(g \circ f=(x-1)(x+3)=x^2+2x-3\)
3.6. Razona cuál de las siguientes figuras corresponde con la gráfica de la función \(f(x)\).
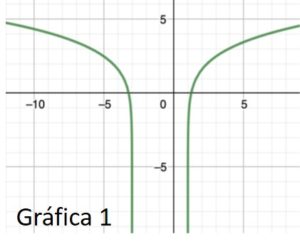
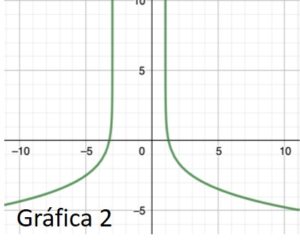
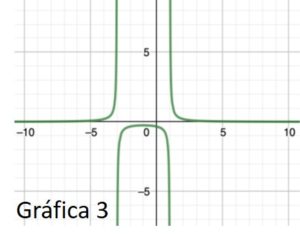
Solución
La figura 1, que es la única que concuerda con todos los datos obtenidos.
4. (2 puntos) La siguiente figura proporciona la gráfica de \(f'(x)\), que es la derivada de una función desconocida \(f(x)\). Contesta razonadamente las siguientes preguntas:
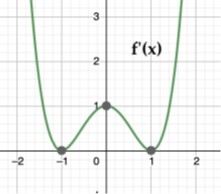
4.1. Razona las zonas de crecimiento y decrecimiento de \(f(x)\).
Solución
\(f(x)\) es siempre creciente, pues \(f'(X)>0 \ \forall x\)
4.2. Razona dónde alcanza \(f(x)\) máximos y/o mínimos locales, en caso de que existan.
Solución
\(f(x)\) solo puede tener máximos y/o mínimos locales en los puntos donde \(f'(x)=0\).
No obstante, al no haber cambio de signo de \(f'(x)\) no hay máximos ni mínimos locales. Habrá «puntos de rellano».
4.3. Razona la concavidad o convexidad de \(f(x)\) en el intervalo \( (-\infty,-1) \).
Solución
Cóncava en \( (-\infty, -1) \cup (0,1) \)
Convexa en \( (-1,0) \cup (1,+\infty) \)
4.4. Razona si \(f(x)\) tiene puntos de inflexión (indicando, si los hay, los valores de \(x\) donde se alcanzan).
Solución
Puntos de inflexión en \(x=-1, \ x=0, \ x=1\) que es donde la función cambia su concavidad.
4.5. Si se sabe que la función \(y = f(x)\) es solución de la ecuación diferencial \(\dfrac{y’}{x^2-1}=x^2-1\)
que cumple \(f(0) = 0\), calcula \(f(x)\).
Solución
\(y=f(x)=\dfrac{x^5}{5}-\dfrac{2}{3}x^3+x\)
4.6. Si \(f'(x) = x^4 – 2x^2 + 1\), calcula el área entre \(f'(x)\) y el eje \(X\) en el intervalo [-1, 1].
Solución
\(\displaystyle{\int_{-1}^{1}f'(x)dx=\dfrac{16}{15}}\)
5. (2 puntos) Contesta razonadamente las siguientes preguntas:
5.1. Calcula la primitiva de la función \(f(x) = 2x \ln(x^2)\).
Solución
\(F(x)=\displaystyle{\int} f(x) dx=x^2( \ln (x^2)-1)+C\)
5.2. Calcula la primitiva de la función \(f(x) = xe^{x^2}\).
Solución
\(F(x)=\displaystyle{\int} f(x) dx=\dfrac{1}{2}e^{x^2}+C\)
5.3. Calcula, si es convergente, el valor de la integral impropia \(\displaystyle{\int_{1}^{+\infty}}\dfrac{1}{x^3}dx\).
Solución
\(\displaystyle{\int_{1}^{+\infty}}\dfrac{1}{x^3}dx=\dfrac{1}{2}\)
5.4. Calcula el intervalo abierto de convergencia de la serie de potencias \(\displaystyle{\sum_{i=1}^{+\infty}}\dfrac{1}{n}\dfrac{1}{2^n}x^n\).
Solución
\( (-2,2) \)
5.5. Analiza si en los extremos del intervalo abierto de convergencia de la serie de potencias del apartado anterior, las series numéricas son convergentes.
Solución
En \(x=-2\) la serie queda \(\displaystyle{\sum_{i=1}^{\infty}}\frac{1}{n}\frac{1}{2^n}(-2^n)=\sum_{i=1}^{\infty}\frac{1}{n}(-1)^n\) que es una serie armónica alternada que sabemos que converge siempre.
En \(x=2\) la serie queda \(\displaystyle{\sum_{i=1}^{\infty}}\frac{1}{x}\frac{1}{2^n}2^n=\displaystyle{\sum_{i=1}^{\infty}}\frac{1}{x}\) que es la serie armónica que sabemos que es divergente.
5.6. Indica la razón de la serie geométrica \(\displaystyle{\sum_{i=1}^{\infty}}\dfrac{(2)^{2n}}{(-3)^n}\)y, en caso de que sea convergente, calcula su suma.
Solución
\(r=-\dfrac{4}{3}\)
\(|r|>1\) : La serie es divergente
